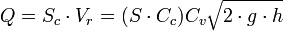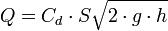Milán, 1598- Bolonia, 1647
Jesuita y matemático italiano, fue alumno de Galileo Galilei, y enseñó matemáticas en Bolonia (1629). Su interés por las matemáticas fue estimulado por los trabajos de Euclides.
Fue el primero en introducir en Italia el cálculo logarítmico, pero debe su celebridad a su teoría de los «indivisibles», que expuso en Geometría indivisibilibus continuorum quadam nova ratione promota (1635). Esta teoría estudia las magnitudes geométricas como compuestas de un número infinito de elementos, o indivisibles, que son los últimos términos de la descomposición que se puede hacer. La medida de las longitudes, de las superficies y de los volúmenes se convierte en efectuar la suma de la infinidad de indivisibles: es el principio del cálculo de una integral definida, aunque sin la noción rigurosa moderna de paso al límite. Por esto puede ser considerado como uno de los precursores del análisis infinitesimal moderno.
EL PRINCIPIO DE CAVALIERI
"Si dos cuerpos tienen la misma altura y además tienen igual área en sus secciones planas realizadas a una misma altura, poseen entonces igual volumen"
Bienvenidos a nuestro blog. En él viviréis un viaje a través de la Ciencia, desde sus orígenes hasta los conceptos y descubrimientos más recientes. Para disfrutarlo conviene comenzar en la entrada más antigua e ir avanzando cronológicamente. Además, habrá algunas etapas en las que se nombren algunos conceptos, experimentos o demostraciones interesantes en los que basta un sólo clic para adentrarse más profundamente en ellos. Sin más, agradeceros vuestra visita y desearos un feliz viaje.
martes, 8 de febrero de 2011
Gilles Personne de Roberval
Fue un matemático nacido el 10 de agosto de 1602 en Senlis, Francia. No es casual que sea considerado uno de los matemáticos más importantes de la historia, puesto que comenzó con sus estudios de manera muy precoz. Como su espíritu era muy inquieto, no se contentaba con quedarse abocado a los libros en su lugar natal, sino que además buscaba realizar permanentes viajes por toda Francia.
En 1632, con 30 años,comenzaba su etapa de éxitos. Primero fue nombrado como profesor de la Universidad Gervais – también en París – y dos años más tarde obtuvo un puesto muy prestigioso y codiciado: el de presidente matemático de otra universidad, la denominada Royale. Pero aquí no se acabaron sus cosechas. En 1666 fue elegido como miembro fundador de la Academia Real de Ciencias.
EL MECANISMO DE ROBERVAL
Fue en 1669 cuando pudo terminar de concretar su llamado Balance Roberval.
Su aporte radicaba en la invención de un sistema de varios astiles que se podían acoplar siempre y cuando fuera paralelamente (mecanismo de Roberval). Debido a esto, lo que se desafiaba era el ya famoso método de palancas o sistema de palancas, que a su vez permitía que los platos de la balanza se mantuvieran en una horizontalidad que no se pusiera en peligro ni siquiera con el desplazamiento de los pesos.
Lo que proveía el Mecanismo de Roberval era que los platos destinados a la recepción de la mercadería se encontraran sobre la barra de la balanza. Esto se oponía a una colocación perpendicular de los mismos que encontraba su auge en los métodos más tradicionales. Dicho método continúa en boga hoy, incluso en las balanzas de índole electrónica. En este modelo, la flexión de un resorte es lo que permite que un disco codificado comience a rotar y active los denominados detectores fotoeléctricos, a partir de la irradiación de ondas luminosas. Ese disco, a su vez, tiene ciertos códigos y cada uno de ellos se corresponde con un peso determinado.
En 1632, con 30 años,comenzaba su etapa de éxitos. Primero fue nombrado como profesor de la Universidad Gervais – también en París – y dos años más tarde obtuvo un puesto muy prestigioso y codiciado: el de presidente matemático de otra universidad, la denominada Royale. Pero aquí no se acabaron sus cosechas. En 1666 fue elegido como miembro fundador de la Academia Real de Ciencias.
EL MECANISMO DE ROBERVAL
Fue en 1669 cuando pudo terminar de concretar su llamado Balance Roberval.
Su aporte radicaba en la invención de un sistema de varios astiles que se podían acoplar siempre y cuando fuera paralelamente (mecanismo de Roberval). Debido a esto, lo que se desafiaba era el ya famoso método de palancas o sistema de palancas, que a su vez permitía que los platos de la balanza se mantuvieran en una horizontalidad que no se pusiera en peligro ni siquiera con el desplazamiento de los pesos.
Lo que proveía el Mecanismo de Roberval era que los platos destinados a la recepción de la mercadería se encontraran sobre la barra de la balanza. Esto se oponía a una colocación perpendicular de los mismos que encontraba su auge en los métodos más tradicionales. Dicho método continúa en boga hoy, incluso en las balanzas de índole electrónica. En este modelo, la flexión de un resorte es lo que permite que un disco codificado comience a rotar y active los denominados detectores fotoeléctricos, a partir de la irradiación de ondas luminosas. Ese disco, a su vez, tiene ciertos códigos y cada uno de ellos se corresponde con un peso determinado.
Teorema de Torricelli
El Teorema de Torricelli es una aplicación del principio de Bernoulli y estudia el flujo de un líquido contenido en un recipiente, a través de un pequeño orificio, bajo la acción de la gravedad. A partir del teorema de Torricelli se puede calcular el caudal de salida de un líquido por un orificio. "La velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio":
 =1
=1
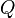 , puede calcularse como el producto de
, puede calcularse como el producto de  , el área real de la sección contraída, por
, el área real de la sección contraída, por 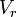 , la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
, la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
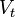 es la velocidad teórica del líquido a la salida del orificio
es la velocidad teórica del líquido a la salida del orificio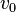 es la velocidad de aproximación.
es la velocidad de aproximación.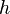 es la distancia desde la superficie del líquido al centro del orificio.
es la distancia desde la superficie del líquido al centro del orificio.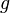 es la aceleración de la gravedad
es la aceleración de la gravedad
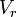 es la velocidad real media del líquido a la salida del orificio
es la velocidad real media del líquido a la salida del orificio es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
 =1
=1Caudal descargado
El caudal o volumen del fluido que pasa por el orificio en un tiempo,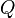 , puede calcularse como el producto de
, puede calcularse como el producto de  , el área real de la sección contraída, por
, el área real de la sección contraída, por 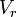 , la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
, la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación: representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.
representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.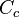 es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior proximas al orificio. Es la relación entre el área contraída
es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior proximas al orificio. Es la relación entre el área contraída  y la del orificio
y la del orificio 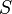 . Suele estar en torno a 0,65.
. Suele estar en torno a 0,65.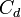 es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes.
es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes. 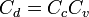
Blaise Pascal
Blaise fue un niño prodigio. Estudió matemáticas, física, teología y filosofía, educado en gran parte por su padre.
Sus primeros trabajos abarcan las ciencias naturales y aplicadas, donde realizó importantes contribuciones para la invención y construcción de calculadoras mecánicas, estudios de la teoría matemática de probabilidad, investigaciones sobre los fluidos y conceptos tales como la presión y el vacío, generalizando la obra de Torricelli, del que ya hemos hablado en otra entrada.
Pascal fue un matemático de primer orden. Ayudó a crear dos grandes áreas de investigación y escribió importantes tratados sobre geometría proyectiva a los 16 años. Siguiendo con el trabajo de Galileo y de Torricelli, en 1646 refutó las teorías aristotélicas que insistían en que la naturaleza aborrece el vacío, y sus resultados causaron grandes discusiones antes de ser generalmente aceptados.
Nos centraremos especialmente en las contribuciones realizadas por este personaje al campo de la física.
Pascal trabajó en los campos de estudio de líquidos (hidrodinámica e hidrostática), centrándose en los principios de fluidos hidráulicos. Entre sus invenciones se incluye la prensa hidráulica (que usa la presión hidráulica para multiplicar la fuerza) y la jeringuilla.
En el año 1646,como ya hemos comentado, Pascal ya conocía los experimentos de Torricelli con barómetros. Tras replicar la creación de un barómetro de mercurio, para lo cual se coloca un tubo de mercurio boca abajo en un recipiente lleno de ese metal, Pascal comenzó a cuestionarse qué fuerza era la que hacía que parte del mercurio se quedase dentro del tubo y qué era lo que llenaba el espacio por encima del mercurio hasta el final del tubo. Por aquella época, la mayoría de los científicos consideraban que existía algún tipo de materia invisible, en lugar de simplemente el vacío. Este pensamiento se basaba en la noción aristotélica de que la creación es algo con sustancia, ya fuera visible o invisible, y que la sustancia está siempre en movimiento. Es más, Aristóteles declaraba que todo lo que está en movimiento debe estar a su vez siendo impulsado por algo. La noción del vacío como tal era una imposibilidad bajo las concepciones de la época.
Sin embargo, y tras una serie de trabajos experimentales en esta línea, en 1647 Pascal publicó Experiences nouvelles touchant le vide ("Nuevos Experimentos sobre el Vacío"), en donde detallaba una serie de reglas básicas que describían hasta qué punto varios líquidos podían estar soportados por la presión del aire. También ofrecía razones por las que lo que había por encima de la columna de líquido era realmente un vacío.
Sus primeros trabajos abarcan las ciencias naturales y aplicadas, donde realizó importantes contribuciones para la invención y construcción de calculadoras mecánicas, estudios de la teoría matemática de probabilidad, investigaciones sobre los fluidos y conceptos tales como la presión y el vacío, generalizando la obra de Torricelli, del que ya hemos hablado en otra entrada.
Pascal fue un matemático de primer orden. Ayudó a crear dos grandes áreas de investigación y escribió importantes tratados sobre geometría proyectiva a los 16 años. Siguiendo con el trabajo de Galileo y de Torricelli, en 1646 refutó las teorías aristotélicas que insistían en que la naturaleza aborrece el vacío, y sus resultados causaron grandes discusiones antes de ser generalmente aceptados.
APORTACIÓN A LA FÍSICA
Nos centraremos especialmente en las contribuciones realizadas por este personaje al campo de la física.
Pascal trabajó en los campos de estudio de líquidos (hidrodinámica e hidrostática), centrándose en los principios de fluidos hidráulicos. Entre sus invenciones se incluye la prensa hidráulica (que usa la presión hidráulica para multiplicar la fuerza) y la jeringuilla.
En el año 1646,como ya hemos comentado, Pascal ya conocía los experimentos de Torricelli con barómetros. Tras replicar la creación de un barómetro de mercurio, para lo cual se coloca un tubo de mercurio boca abajo en un recipiente lleno de ese metal, Pascal comenzó a cuestionarse qué fuerza era la que hacía que parte del mercurio se quedase dentro del tubo y qué era lo que llenaba el espacio por encima del mercurio hasta el final del tubo. Por aquella época, la mayoría de los científicos consideraban que existía algún tipo de materia invisible, en lugar de simplemente el vacío. Este pensamiento se basaba en la noción aristotélica de que la creación es algo con sustancia, ya fuera visible o invisible, y que la sustancia está siempre en movimiento. Es más, Aristóteles declaraba que todo lo que está en movimiento debe estar a su vez siendo impulsado por algo. La noción del vacío como tal era una imposibilidad bajo las concepciones de la época.
Sin embargo, y tras una serie de trabajos experimentales en esta línea, en 1647 Pascal publicó Experiences nouvelles touchant le vide ("Nuevos Experimentos sobre el Vacío"), en donde detallaba una serie de reglas básicas que describían hasta qué punto varios líquidos podían estar soportados por la presión del aire. También ofrecía razones por las que lo que había por encima de la columna de líquido era realmente un vacío.
Gottfried Wilhelm Leibniz
"Lo que llamamos “casualidad” no es más que la ignorancia de las causas físicas."
G.W.Leibniz
 Nace en Leipzig,Alemania el 1 de julio de 1646 y muere en Hannover,Alemania el 14 de noviembre de 1716. Fue uno de los grandes pensadores del siglo XVII y XVIII, y se le reconoce como "El último genio universal". Ocupa un lugar igualmente importante tanto en la historia de la filosofía como en la de las matemáticas.
Nace en Leipzig,Alemania el 1 de julio de 1646 y muere en Hannover,Alemania el 14 de noviembre de 1716. Fue uno de los grandes pensadores del siglo XVII y XVIII, y se le reconoce como "El último genio universal". Ocupa un lugar igualmente importante tanto en la historia de la filosofía como en la de las matemáticas.Inventó el cálculo infinitesimal, junto con Newton, y su notación es la que se emplea desde entonces. También inventó el sistema binario, fundamento de virtualmente todas las arquitecturas de las computadoras actuales.
La invención del cálculo infinitesimal es atribuida tanto a Leibniz como a Newton. De acuerdo con los cuadernos de Leibniz, el 11 de noviembre de 1675 tuvo lugar un acontecimiento fundamental, ese día empleó por primera vez el cálculo integral para encontrar el área bajo la curva de una función y=f(x).
 En 1672 también inventó una máquina de calcular capaz de multiplicar, dividir y extraer raíces cuadradas.
En 1672 también inventó una máquina de calcular capaz de multiplicar, dividir y extraer raíces cuadradas. Es considerado un pionero en el
desarrollo de la lógica matemática y uno de los precursores de los ordenadores.
Los últimos años de su vida, estuvieron ocupados por la disputa con Newton sobre quien había descubierto primero el Cálculo. El debate sobre la 'paternidad' del cálculo infinitesimal fue muy duro y duró varios
años.
El científico que revolucionó la historia: Newton
"Platón es mi amigo, Aristóteles es mi amigo, pero mi mejor amiga es la verdad"
Isaac Newton
Sir Isaac Newton (4 de enero de 1643 – 31 de marzo de 1727 ) fue un físico, filósofo, teólogo, inventor, alquimista y matemático inglés, autor de los Philosophiae naturalis principia mathematica, más conocidos como los Principia, donde describió la ley de gravitación universal.
La manzana que cae
La gravedad se extiende por todo el universo, según Isaac Newton , que obtuvo esta idea cuando estaba sentado bajo un manzano . Newton entendía el concepto de inercia de Galileo, sabía que en ausencia de fuerzas externas los objetos se conservan en movimiento o en línea recta con rapidez constante . También sabía que todo cambio en la rapidez o dirección de un objeto se debe a la acción de una fuerza .
Newton había estado reflexionando acerca del hecho de que la Luna no describe una trayectoria recta , sino, gira alrededor de la Tierra y también que , un movimiento circular es un movimiento acelerado, lo que implica la presencia de una fuerza ; esta fuerza se desconocía .
Newton tubo la perspicacia de comprender que la fuerza que actúa entre la Tierra y la Luna es la misma fuerza que tira de todas la manzanas y de todas las cosas a la que llamó fuerza de gravedad.
Hallazgos Científicos:
Entre sus hallazgos científicos se encuentran:

-El descubrimiento de que el espectro de color que se observa cuando la luz blanca pasa por un prisma es inherente a esa luz.
-Su argumentación sobre la posibilidad de que la luz estuviera compuesta por partículas.
 -Su desarrollo de una ley de convección térmica, que describe la tasa de enfriamiento de los objetos expuestos al aire.
-Su desarrollo de una ley de convección térmica, que describe la tasa de enfriamiento de los objetos expuestos al aire. -Sus estudios sobre la velocidad del sonido en el aire.
-Su propuesta de una teoría sobre el origen de las estrellas, y publicación posterior de sus ''Principia'' en 1687.
Fue también un pionero de la mecánica de fluidos, estableciendo una ley sobre la viscosidad. A Newton le debemos toda la explicación de la Gravitación universal, todas las explicaciones de la gravedad, y la fuerza entre cuerpos.
Las Leyes de Newton son tres principios concernientes al movimiento de los cuerpos. Las leyes de Newton constituyen, junto con la transformación
de Galileo, la base de la mecánica clásica.
1ª Ley de Newton o Ley de inercia.
''Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.''
(Isaac Newton, Principia) enlaceUn cuerpo no puede cambiar por sí solo su estado inicial, ya sea en reposo o en movimiento rectilíneo uniforme, a menos que se aplique una fuerza o una serie de fuerzas cuyo resultante no sea nulo sobre él.
2ª Ley de Newton o Ley de Fuerza
''El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.''
(Isaac Newton, Principia) enlace
Esta ley explica qué ocurre si sobre un cuerpo en movimiento actúa una fuerza: la fuerza modificará el estado de movimiento, cambiando la velocidad en módulo o dirección. Consecuentemente, hay relación la fuerza y la aceleración.
De esta ley deducimos que: F=ma
3ª Ley de Newton o Ley de acción-reacción.
''Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.''
(Isaac Newton, Principia) enlaceLa tercera ley es completamente original de Newton (pues las dos primeras ya habían sido propuestas de otras maneras por Galileo, Hookey Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo.7 Expone que por cada fuerza que actúa sobre un cuerpo, este realiza una fuerza de igual intensidad y dirección, pero de sentido contrario sobre el cuerpo que la produjo.
La acción del aire sobre el ala del avión provoca una reacción de elevación del avión
Newton y los agujeros negros.
Devienen de procesos que se llevan a
Es posible que el campo gravitacional del los agujeros negros sea enorme , no alterándose por la contracción el campo gravitacional de las estrellas mas cercanas.
Los agujeros negros serán una pesadilla para los astronautas del futuro, el mejor consejo que nos da este capítulo es que no se acerquen a ellos , pues la configuración del campo gravitacional en la vecindad de un agujero negro representa el colapso del propio espacio.
Campo gravitatorio en un agujero negro
La bomba de Vacío, un invento del S. XVII
Una bomba de vacío extrae moléculas de gas de un volumen sellado, para crear un vacío parcial. La bomba de vacío fue inventada en 1650 por Otto von Guericke, estimulado por el trabajo de Galileo y Torricelli, usando los Hemisferios de Magdeburgo.
Otto von Guerick estudió los tratados de Blaise Pascal y Torricelli sobre la presión atmosférica. En 1654, Von Guericke gracias a la bomba de vacío hizo una espectacular demostración de la inmensa fuerza que la atmósfera podía ejercer. Mostró que cuando dos hemisferios de cobre de 50 centímetros de diámetro perfectamente ajustados eran unidos de manera que formasen una esfera y se hacía el vacío en su interior, ocho caballos tirando de la esfera no podían separarlos.
Otto von Guerick estudió los tratados de Blaise Pascal y Torricelli sobre la presión atmosférica. En 1654, Von Guericke gracias a la bomba de vacío hizo una espectacular demostración de la inmensa fuerza que la atmósfera podía ejercer. Mostró que cuando dos hemisferios de cobre de 50 centímetros de diámetro perfectamente ajustados eran unidos de manera que formasen una esfera y se hacía el vacío en su interior, ocho caballos tirando de la esfera no podían separarlos.
Un científico centrífugo: Christiaan Huygens
"El mundo es mi patria, la ciencia mi religión".
Christiaan HuygensAstrónomo, físico y matemático neolandés. Estudió mecánica y geometría, y tuvo influencia de gente como Descartes o Newton.
En cuanto a su obra, fue uno de los pioneros en cálculos de probabilidad y derivadas, pero nos centraremos más en sus avances científicos.
FÍSICA
Los trabajos de Huygens en Física se centraron principalmente en dos campos: la mecánica y la óptica. En el campo de la mecánica publicó su libro Horologium oscillatorum (1675), en el se halla la expresión exacta de la fuerza centrífuga en un movimiento circular, la teoría del centro de oscilación, el principio de la conservación de las fuerzas vivas (antecedente del principio de la conservación de la energía centrándose esencialmente en las colisiones entre partículas) y el funcionamiento del péndulo simple y del reversible.

En el campo de la óptica elaboró la teoría ondulatoria de la luz, partiendo del concepto de que cada punto luminoso de un frente de ondas puede considerarse una nueva fuente de ondas (Principio de Huygens).
A partir de esta teoría explicó, en su obra Traité de la lumière, la reflexión, refracción y doble refracción de la luz. Dicha teoría quedó definitivamente demostrada por los experimentos de Thomas Young, a principios del siglo XIX.
ASTRONOMÍA
Aficionado a la astronomía desde pequeño, pronto aprendió a tallar lentes (especialidad de Holanda desde la invención del telescopio, hacia el año 1608) y junto a su hermano llegó a construir varios telescopios de gran calidad. Por el método de ensayo y error comprobaron que los objetivos de gran longitud focal proporcionaban mejores imágenes, de manera que se dedicó a construir instrumentos de focales cada vez mayores.
En 1655 terminó un telescopio de gran calidad, lo que le permitía obtener unos cincuenta aumentos. Con este aparato vio que en torno al planeta Saturno existía un anillo (descubierto por Galileo con anterioridad que no pudo identificarlo claramente) y la existencia de un satélite, Titán, el 25 de marzo de ese año. Después de seguirlo durante varios meses, para estar seguro de su período y órbita, dio a conocer la noticia en 1656.
Continuó con la fabricación y pulido de lentes con focales cada vez mayores. Terminó un telescopio con una focal de 37 metros. Instalado sobre largos postes, sostenido por cuerdas para evitar el alabeo de la madera, con él llegó a obtener una imagen muy clara de los anillos de Saturno, llegando a divisar la sombra que arrojaban sobre el planeta. También estudió el cambio en la forma e iluminación de los anillos a medida que el planeta giraba alrededor del Sol.
En honor suyo, la sonda enviada a Titán lleva su nombre.
Periodos de Júpiter
Torricelli
''Vivimos en un fondo de mar de aire''
Evangelista Torricelli
Evangelista Torricelli (Faenza, Italia, 15 de octubre 1608 - Florencia, Italia, 25 de octubre 1647) fue un físico y matemático italiano. Fue uno de los primeros discípulos de Galileo.
 En 1643 realizó el descubrimiento que lo haría pasar a la posteridad: el principio del barómetro, que demostraba la existencia de la presión atmosférica, principio confirmado posteriormente por Pascal realizando mediciones a distinta altura. Aunque el mencionado experimento ha pasado a la historia por la importancia del barómetro y de la medida de la presión atmosférica, la motivación inicial tanto de Torricelli como de Pascal para realizar este experimento fue refutar la teoría aristotélica de que que "la naturaleza tiene horror al vacío". La unidad de presión torr se nombró en su memoria. Enunció, además, el Teorema de Torricelli, de importancia fundamental en hidráulica.
En 1643 realizó el descubrimiento que lo haría pasar a la posteridad: el principio del barómetro, que demostraba la existencia de la presión atmosférica, principio confirmado posteriormente por Pascal realizando mediciones a distinta altura. Aunque el mencionado experimento ha pasado a la historia por la importancia del barómetro y de la medida de la presión atmosférica, la motivación inicial tanto de Torricelli como de Pascal para realizar este experimento fue refutar la teoría aristotélica de que que "la naturaleza tiene horror al vacío". La unidad de presión torr se nombró en su memoria. Enunció, además, el Teorema de Torricelli, de importancia fundamental en hidráulica.En 1644 publicó su trabajo sobre el movimiento bajo el título Opera geometrica. La publicación, junto a esta obra, de varios trabajos sobre las propiedades de las curvas cicloides le supuso una agria disputa con Roberval, quien le acusó de plagiar sus soluciones del problema de la cuadratura de dichas curvas. Aunque no parece haber dudas de que Torricelli llegó al mismo resultado de forma independiente, el debate sobre la primicia de la solución se prolongó hasta su muerte.
Entre los descubrimientos que realizó, se encuentra el principio que dice que si una serie de cuerpos están conectados de modo tal que, debido a su movimiento, su centro de gravedad no puede ascender o descender, entonces dichos cuerpos están en equilibrio.
Descubrió además que la envolvente de todas las trayectorias parabólicas descritas por los proyectiles lanzados desde un punto con igual velocidad, pero en direcciones diferentes, es un paraboloide de revolución. Así mismo, empleó y perfeccionó el método de los indivisibles de Cavalieri.
También realizó importantes mejoras en el telescopio y el microscopio, siendo numerosas las lentes por él fabricadas y grabadas con su nombre que aún se conservan en Florencia.
Experimento de Torricelli
Suscribirse a:
Comentarios (Atom)